I just pushed a new
phytools update to GitHub. It primarily involves the addition of an S3 plotting method to the function
fitpolyMk that I described a
couple of days ago, but also fixes a small bug in fitpolyMk itself.
Just to review, this function fits an extended Mk to data that include intraspecific polymorphism. The basic idea is that if we imagine two states, A and B, evolution from A to B must occur through the intermediate polymorphic condition of A + B. If we extend this logic to more than two states then we must decide if evolution is ordered (i.e., A ↔ A + B ↔ B ↔ B + C ↔ C, and so on) or unordered, in which case we might suppose that multistate polymorphism (e.g., A + B + C) can also occur with some probability.
When I first tried to envision a plotting method for this function I tried to design a circular graph similar to what I
previously developed for
fitMk. For instance, here is a beta attempt I posted to my Facebook page:
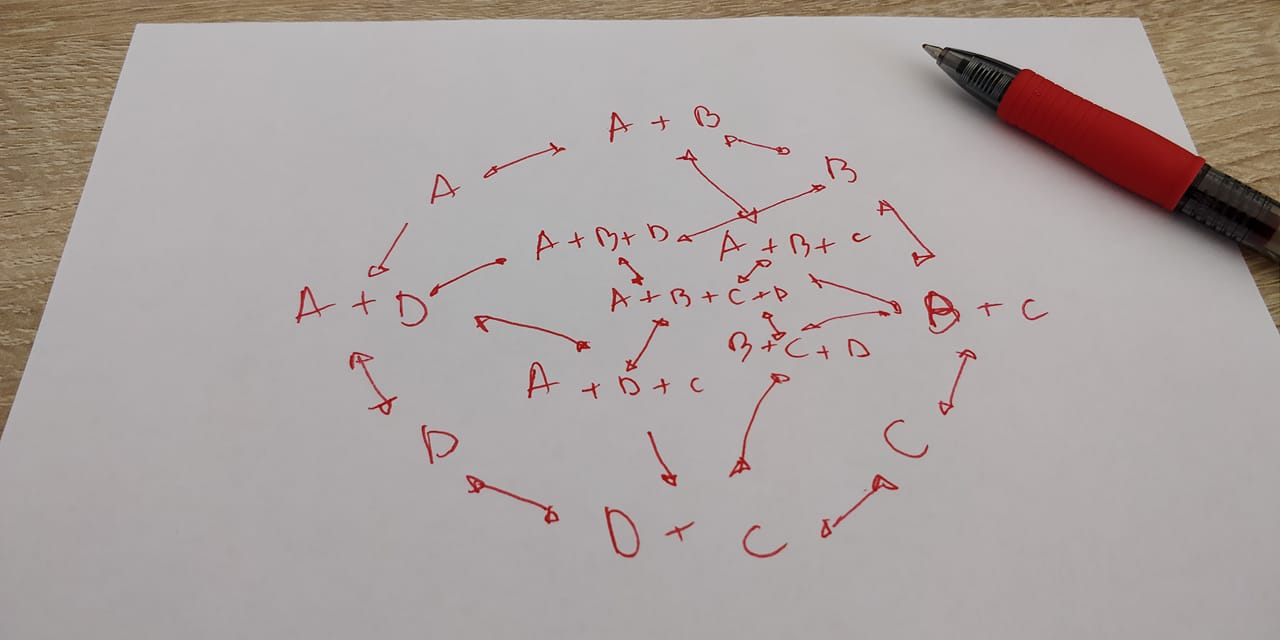
Unfortunately, this type of design becomes very messy & not so easy to interpret for even a relatively small number of character states.
Instead, I ultimately settled on a circular design for the ordered model, but a more-or-less 'vertical' design for the unordered polymorphic transition model, which I'll show in a moment.
Here, once again I'm going to demonstrate the fitting & plotting methods using simulated polymorphic discrete character data. Perhaps it's also worth noting that we don't have to observe all possible polymorphic conditions in our data to fit a model in which these conditions can exist!
First, let's load our updated version of phytools:
library(phytools)
packageVersion("phytools")
## [1] '0.6.68'
Now we'll work with a set of simulated datasets. For now, there is no way of specifying order in the 'ordered' model: it is assumed to be alphanumeric. (I intend to update this later, but it seems like a relatively minor inconvenience.)
Let's start by looking at our first data vector & tree, x & tree, respectively, and then plotting these data
on the phylogeny:
tree
##
## Phylogenetic tree with 200 tips and 199 internal nodes.
##
## Tip labels:
## t103, t104, t197, t198, t74, t75, ...
##
## Rooted; includes branch lengths.
x
## t103 t104 t197 t198 t74 t75 t53 t85 t132 t185 t186 t64
## A A A A B B B A+B A A A B
## t87 t94 t136 t137 t148 t149 t27 t78 t79 t187 t188 t163
## B B B B B B B B A+B+C A+B B B
## t164 t38 t39 t72 t73 t4 t116 t117 t43 t42 t139 t140
## B B B B B B B A+B B B B B
## t195 t196 t165 t41 t109 t179 t180 t146 t147 t100 t99 t174
## B B B B B+C B B B+C B+C B+C A+C B
## t175 t50 t60 t61 t44 t15 t16 t7 t152 t153 t199 t200
## B B+C C B B B A+C A B B B B
## t159 t160 t59 t90 t91 t34 t110 t111 t82 t22 t70 t71
## B B B B B B C C C B+C A+B B
## t21 t30 t31 t20 t62 t63 t127 t128 t95 t96 t46 t129
## B A B B+C B B A A B B B B+C
## t130 t114 t115 t67 t23 t24 t57 t58 t11 t154 t176 t177
## A+B+C A+C C A+C B B B B A+B B B B
## t138 t191 t192 t178 t6 t29 t125 t126 t45 t54 t189 t190
## B B B B C B B B+C A+B A+B B B
## t112 t113 t65 t66 t32 t33 t181 t182 t161 t162 t121 t105
## B B B B B B B B B B B B
## t106 t157 t158 t92 t93 t76 t77 t84 t150 t151 t143 t3
## B B+C B+C B A+B+C B B B B B B C
## t12 t13 t51 t52 t107 t108 t37 t25 t26 t2 t9 t10
## B B C B B+C B A+B A+B A B B+C B
## t18 t19 t8 t28 t36 t48 t86 t155 t156 t81 t88 t89
## A A+B C B B A+B+C C C C A A A
## t172 t173 t49 t17 t141 t142 t131 t101 t102 t35 t68 t69
## A A A C A+B A+B A+B A A A A A
## t166 t167 t122 t123 t119 t120 t14 t55 t56 t47 t124 t183
## A A+B A+C C C C C A A+B+C C C C
## t184 t168 t169 t134 t135 t83 t170 t171 t40 t144 t145 t80
## C C C C C C A A A+C C A C
## t193 t194 t133 t118 t5 t1 t97 t98
## A A A A C B C C
## Levels: A A+B A+B+C A+C B B+C C
plotTree(tree,ftype="off",lwd=1,type="fan")
X<-strsplit(setNames(as.character(x),names(x)),"+",fixed=TRUE)
pies<-matrix(0,Ntip(tree),3,dimnames=list(tree$tip.label,c("A","B","C")))
for(i in 1:Ntip(tree))
pies[tree$tip.label[i],X[[tree$tip.label[i]]]]<-rep(1/length(X[[tree$tip.label[i]]]),
length(X[[tree$tip.label[i]]]))
tiplabels(pie=pies,piecol=c("black","yellow","red"),cex=0.35)
legend(x="topleft",legend=c("A","B","C"),pt.cex=2,pch=21,
pt.bg=c("black","yellow","red"))
Next, what I'm going to do is fit a few different models to the data and compare them, just as I did in my
previous post. Note that for character
x we must fit an 'unordered' model because the multistate polymorphic condition (A+B+C in
this case) exists in our data.
ard.unordered<-fitpolyMk(tree,x,model="ARD")
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A B C A+B A+C B+C A+B+C
## A 0 0 0 1 3 0 0
## B 0 0 0 5 0 7 0
## C 0 0 0 0 9 11 0
## A+B 2 6 0 0 0 0 13
## A+C 4 0 10 0 0 0 15
## B+C 0 8 12 0 0 0 17
## A+B+C 0 0 0 14 16 18 0
ard.unordered
## Object of class "fitpolyMk".
##
## Evolution was modeled as 'unordered' using the "ARD" model.
##
## Fitted (or set) value of Q:
## A B C A+B A+C B+C
## A -0.958476 0.000000 0.000000 0.958476 0.000000 0.000000
## B 0.000000 -1.871278 0.000000 0.654131 0.000000 1.217148
## C 0.000000 0.000000 -7.424279 0.000000 7.424279 0.000000
## A+B 3.519568 2.210898 0.000000 -5.730466 0.000000 0.000000
## A+C 6.287675 0.000000 32.728264 0.000000 -42.921115 0.000000
## B+C 0.000000 6.194701 2.114481 0.000000 0.000000 -13.379396
## A+B+C 0.000000 0.000000 0.000000 0.000000 8.116189 10.849789
## A+B+C
## A 0.000000
## B 0.000000
## C 0.000000
## A+B 0.000000
## A+C 3.905176
## B+C 5.070214
## A+B+C -18.965978
##
## Fitted (or set) value of pi:
## A B C A+B A+C B+C A+B+C
## 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571
##
## Log-likelihood: -198.978338
##
## Optimization method used was "nlminb"
sym.unordered<-fitpolyMk(tree,x,model="SYM")
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A B C A+B A+C B+C A+B+C
## A 0 0 0 1 2 0 0
## B 0 0 0 3 0 4 0
## C 0 0 0 0 5 6 0
## A+B 1 3 0 0 0 0 7
## A+C 2 0 5 0 0 0 8
## B+C 0 4 6 0 0 0 9
## A+B+C 0 0 0 7 8 9 0
sym.unordered
## Object of class "fitpolyMk".
##
## Evolution was modeled as 'unordered' using the "SYM" model.
##
## Fitted (or set) value of Q:
## A B C A+B A+C B+C
## A -3.775788 0.000000 0.000000 2.254469 1.521320 0.000000
## B 0.000000 -1.592209 0.000000 0.646719 0.000000 0.945491
## C 0.000000 0.000000 -6.519037 0.000000 4.204605 2.314431
## A+B 2.254469 0.646719 0.000000 -2.901187 0.000000 0.000000
## A+C 1.521320 0.000000 4.204605 0.000000 -6.429092 0.000000
## B+C 0.000000 0.945491 2.314431 0.000000 0.000000 -5.719308
## A+B+C 0.000000 0.000000 0.000000 0.000000 0.703167 2.459386
## A+B+C
## A 0.000000
## B 0.000000
## C 0.000000
## A+B 0.000000
## A+C 0.703167
## B+C 2.459386
## A+B+C -3.162553
##
## Fitted (or set) value of pi:
## A B C A+B A+C B+C A+B+C
## 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571
##
## Log-likelihood: -224.236358
##
## Optimization method used was "nlminb"
transient.unordered<-fitpolyMk(tree,x,model="transient")
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A B C A+B A+C B+C A+B+C
## A 0 0 0 2 2 0 0
## B 0 0 0 2 0 2 0
## C 0 0 0 0 2 2 0
## A+B 1 1 0 0 0 0 2
## A+C 1 0 1 0 0 0 2
## B+C 0 1 1 0 0 0 2
## A+B+C 0 0 0 1 1 1 0
transient.unordered
## Object of class "fitpolyMk".
##
## Evolution was modeled as 'unordered' using the "transient" model.
##
## Fitted (or set) value of Q:
## A B C A+B A+C B+C
## A -1.918232 0.000000 0.000000 0.959116 0.959116 0.000000
## B 0.000000 -1.918232 0.000000 0.959116 0.000000 0.959116
## C 0.000000 0.000000 -1.918232 0.000000 0.959116 0.959116
## A+B 3.876625 3.876625 0.000000 -8.712366 0.000000 0.000000
## A+C 3.876625 0.000000 3.876625 0.000000 -8.712366 0.000000
## B+C 0.000000 3.876625 3.876625 0.000000 0.000000 -8.712366
## A+B+C 0.000000 0.000000 0.000000 3.876625 3.876625 3.876625
## A+B+C
## A 0.000000
## B 0.000000
## C 0.000000
## A+B 0.959116
## A+C 0.959116
## B+C 0.959116
## A+B+C -11.629875
##
## Fitted (or set) value of pi:
## A B C A+B A+C B+C A+B+C
## 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571
##
## Log-likelihood: -208.806632
##
## Optimization method used was "nlminb"
er.unordered<-fitpolyMk(tree,x,model="ER")
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A B C A+B A+C B+C A+B+C
## A 0 0 0 1 1 0 0
## B 0 0 0 1 0 1 0
## C 0 0 0 0 1 1 0
## A+B 1 1 0 0 0 0 1
## A+C 1 0 1 0 0 0 1
## B+C 0 1 1 0 0 0 1
## A+B+C 0 0 0 1 1 1 0
er.unordered
## Object of class "fitpolyMk".
##
## Evolution was modeled as 'unordered' using the "ER" model.
##
## Fitted (or set) value of Q:
## A B C A+B A+C B+C
## A -2.467694 0.000000 0.000000 1.233847 1.233847 0.000000
## B 0.000000 -2.467694 0.000000 1.233847 0.000000 1.233847
## C 0.000000 0.000000 -2.467694 0.000000 1.233847 1.233847
## A+B 1.233847 1.233847 0.000000 -3.701541 0.000000 0.000000
## A+C 1.233847 0.000000 1.233847 0.000000 -3.701541 0.000000
## B+C 0.000000 1.233847 1.233847 0.000000 0.000000 -3.701541
## A+B+C 0.000000 0.000000 0.000000 1.233847 1.233847 1.233847
## A+B+C
## A 0.000000
## B 0.000000
## C 0.000000
## A+B 1.233847
## A+C 1.233847
## B+C 1.233847
## A+B+C -3.701541
##
## Fitted (or set) value of pi:
## A B C A+B A+C B+C A+B+C
## 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571
##
## Log-likelihood: -233.190591
##
## Optimization method used was "nlminb"
As I did earlier, we can similarly compare among models using AIC:
data.frame(transition_model=c("ARD","SYM","transient","ER"),
logLik=c(logLik(ard.unordered),logLik(sym.unordered),
logLik(transient.unordered),logLik(er.unordered)),
k=c(attr(AIC(ard.unordered),"df"),attr(AIC(sym.unordered),"df"),
attr(AIC(transient.unordered),"df"),attr(AIC(er.unordered),"df")),
AIC=c(AIC(ard.unordered),AIC(sym.unordered),AIC(transient.unordered),
AIC(er.unordered)))
## transition_model logLik k AIC
## 1 ARD -198.9783 18 433.9567
## 2 SYM -224.2364 9 466.4727
## 3 transient -208.8066 2 421.6133
## 4 ER -233.1906 1 468.3812
Now we can also visualize these fitted models. Here are plots of the two best-fitting models: "ARD" and the
"transient" model.
plot(ard.unordered,main="Fitted ARD \'unordered\' model:")
plot(transient.unordered,main="Fitted \'transient\' model:")
Pretty neat, right?
Next, let's look at a 4-state character with intraspecific polymorphism. Here (for simplicity) I'll just presume
an "ER" process and ask whether the data support the 'ordered' or 'unordered' model:
## plot data
plotTree(tree,ftype="off",lwd=1,type="fan")
X<-strsplit(setNames(as.character(y),names(y)),"+",fixed=TRUE)
pies<-matrix(0,Ntip(tree),4,dimnames=list(tree$tip.label,c("A","B","C","D")))
for(i in 1:Ntip(tree))
pies[tree$tip.label[i],X[[tree$tip.label[i]]]]<-rep(1/length(X[[tree$tip.label[i]]]),
length(X[[tree$tip.label[i]]]))
tiplabels(pie=pies,piecol=c("black","yellow","red","blue"),cex=0.35)
legend(x="topleft",legend=c("A","B","C","D"),pt.cex=2,pch=21,
pt.bg=c("black","yellow","red","blue"))
## fit models:
er.ordered<-fitpolyMk(tree,y,model="ER",ordered=TRUE)
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A A+B B B+C C C+D D
## A 0 1 0 0 0 0 0
## A+B 1 0 1 0 0 0 0
## B 0 1 0 1 0 0 0
## B+C 0 0 1 0 1 0 0
## C 0 0 0 1 0 1 0
## C+D 0 0 0 0 1 0 1
## D 0 0 0 0 0 1 0
er.unordered<-fitpolyMk(tree,y,model="ER")
##
## This is the design matrix of the fitted model. Does it make sense?
##
## A B C D A+B A+C A+D B+C B+D C+D A+B+C A+B+D A+C+D B+C+D A+B+C+D
## A 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0
## B 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0
## C 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0
## D 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0
## A+B 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0
## A+C 1 0 1 0 0 0 0 0 0 0 1 0 1 0 0
## A+D 1 0 0 1 0 0 0 0 0 0 0 1 1 0 0
## B+C 0 1 1 0 0 0 0 0 0 0 1 0 0 1 0
## B+D 0 1 0 1 0 0 0 0 0 0 0 1 0 1 0
## C+D 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0
## A+B+C 0 0 0 0 1 1 0 1 0 0 0 0 0 0 1
## A+B+D 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1
## A+C+D 0 0 0 0 0 1 1 0 0 1 0 0 0 0 1
## B+C+D 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1
## A+B+C+D 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0
data.frame(transition_model=c("ER","ER"),
ordered=c("yes","no"),
logLik=c(logLik(er.ordered),logLik(er.unordered)),
k=c(attr(AIC(er.ordered),"df"),attr(AIC(er.unordered),"df")),
AIC=c(AIC(er.ordered),AIC(er.unordered)))
## transition_model ordered logLik k AIC
## 1 ER yes -149.8048 1 301.6096
## 2 ER no -189.3070 1 380.6141
Clearly here the 'ordered' model is much better supported than the 'unordered' model here, but for fun let's still
plot each of them. Here, I'll change the line colors using par (I plan to add this as a built-in feature of the plotting
method in future versions):
par(fg=make.transparent("blue",0.5))
plot(er.ordered,main="Fitted ER \'ordered\' model:",lwd=2)
par(fg=make.transparent("blue",0.5))
plot(er.unordered,main="Fitted ER \'unordered\' model:",lwd=2)
par(fg="black")
Finally, let's take a look at a 5-state polymorphic trait. Once again, for simplicity, I'll presume a "transient"
model & compare 'ordered' and 'unordered' versions of it. I'll also test these against the simpler "ER"
equivalents:
z
## t103 t104 t197 t198 t74 t75 t53 t85 t132 t185 t186 t64 t87 t94 t136
## D D D D B+C B+C B C C C C C C C C
## t137 t148 t149 t27 t78 t79 t187 t188 t163 t164 t38 t39 t72 t73 t4
## C C C A B B B B B B A+B B B B D
## t116 t117 t43 t42 t139 t140 t195 t196 t165 t41 t109 t179 t180 t146 t147
## C C C+D D D D D D D B B B B B B
## t100 t99 t174 t175 t50 t60 t61 t44 t15 t16 t7 t152 t153 t199 t200
## B A C C B B B C+D C C C B+C C B+C B+C
## t159 t160 t59 t90 t91 t34 t110 t111 t82 t22 t70 t71 t21 t30 t31
## B+C B+C B B B B B+C B B B+C B B D C B+C
## t20 t62 t63 t127 t128 t95 t96 t46 t129 t130 t114 t115 t67 t23 t24
## D D D D D C C C C C D C C C C+D
## t57 t58 t11 t154 t176 t177 t138 t191 t192 t178 t6 t29 t125 t126 t45
## B+C B B+C D D D C+D D D D D D D D D
## t54 t189 t190 t112 t113 t65 t66 t32 t33 t181 t182 t161 t162 t121 t105
## D+E E E B+C C C C D C C C C C C C
## t106 t157 t158 t92 t93 t76 t77 t84 t150 t151 t143 t3 t12 t13 t51
## B+C C C C C A+B B C+D C+D D C+D B B+C B D
## t52 t107 t108 t37 t25 t26 t2 t9 t10 t18 t19 t8 t28 t36 t48
## C C+D C B B A+B B A+B A+B B A C C C+D C
## t86 t155 t156 t81 t88 t89 t172 t173 t49 t17 t141 t142 t131 t101 t102
## C C C D D D+E D D D D D D D D D
## t35 t68 t69 t166 t167 t122 t123 t119 t120 t14 t55 t56 t47 t124 t183
## D D D D D D D D D D D D D D+E D
## t184 t168 t169 t134 t135 t83 t170 t171 t40 t144 t145 t80 t193 t194 t133
## D D D D D D C+D C+D E D D D D D D
## t118 t5 t1 t97 t98
## D D C C C
## Levels: A A+B B B+C C C+D D D+E E
transient.unordered<-fitpolyMk(tree,z,model="transient",quiet=TRUE)
transient.ordered<-fitpolyMk(tree,z,model="transient",ordered=TRUE,quiet=TRUE)
er.unordered<-fitpolyMk(tree,z,model="ER",quiet=TRUE)
er.ordered<-fitpolyMk(tree,z,model="ER",ordered=TRUE,quiet=TRUE)
data.frame(transition_model=c("transient","transient","ER","ER"),
ordered=c("no","yes","no","yes"),
logLik=c(logLik(transient.unordered),logLik(transient.ordered),
logLik(er.unordered),logLik(er.ordered)),
k=c(attr(AIC(transient.unordered),"df"),attr(AIC(transient.ordered),"df"),
attr(AIC(er.unordered),"df"),attr(AIC(er.ordered),"df")),
AIC=c(AIC(transient.unordered),AIC(transient.ordered),
AIC(er.unordered),AIC(er.ordered)))
## transition_model ordered logLik k AIC
## 1 transient no -230.5158 2 465.0316
## 2 transient yes -202.2833 2 408.5667
## 3 ER no -297.6168 1 597.2337
## 4 ER yes -227.6106 1 457.2212
Tbe transient-ordered seems to be best, but let's plot it & the unordered model too:
par(fg=make.transparent("blue",0.5))
plot(transient.unordered,cex.traits=0.8,main="Unordered \'transient\' model:")
plot(transient.ordered,cex.traits=0.8,main="Ordered \'transient\' model:")
Cool. Also, the best-fit models (of the ones we considered) happen to have been the generating models in each case. Here's how the phylogeny & data were simulated:
## pure-birth phylogeny
tree<-pbtree(n=200,scale=1)
## 4-state 'transient' unordered model
Q<-matrix(0,7,7)
rownames(Q)<-colnames(Q)<-c("A","B","C","A+B","A+C","B+C","A+B+C")
Q[1,]<-c(0,0,0,1,1,0,0)
Q[2,]<-c(0,0,0,1,0,1,0)
Q[3,]<-c(0,0,0,0,1,1,0)
Q[4,]<-c(4,4,0,0,0,0,1)
Q[5,]<-c(4,0,4,0,0,0,1)
Q[6,]<-c(0,4,4,0,0,0,1)
Q[7,]<-c(0,0,0,4,4,4,0)
diag(Q)<--rowSums(Q)
x<-sim.Mk(tree,Q)
## 4-state 'ER' ordered
Q<-matrix(c(-1,1,0,0,0,0,0,
1,-2,1,0,0,0,0,
0,1,-2,1,0,0,0,
0,0,1,-2,1,0,0,
0,0,0,1,-2,1,0,
0,0,0,0,1,-2,1,
0,0,0,0,0,1,-1),7,7,byrow=TRUE)
rownames(Q)<-colnames(Q)<-c("A","A+B","B","B+C","C","C+D","D")
y<-sim.Mk(tree,Q)
## 5-state 'ER' ordered
Q<-matrix(c(-1,1,0,0,0,0,0,0,0,
4,-8,4,0,0,0,0,0,0,
0,1,-2,1,0,0,0,0,0,
0,0,4,-8,4,0,0,0,0,
0,0,0,1,-2,1,0,0,0,
0,0,0,0,4,-8,4,0,0,
0,0,0,0,0,1,-2,1,0,
0,0,0,0,0,0,4,-8,4,
0,0,0,0,0,0,0,1,-1),9,9,byrow=TRUE)
rownames(Q)<-colnames(Q)<-c("A","A+B","B","B+C","C","C+D","D","D+E","E")
z<-sim.Mk(tree,Q)
That's all for now!
Liam, all this reminds me of Polymorphism Parsimony, which was explored in the 1960s-1970s and was mentioned in my phylogenies book. Any relation?
ReplyDeleteHi Joe. The implicit model is similar, but it looks like in polymorphism parsimony the derived character state can only be acquired once, whereas here there is no such implicit restriction (unless we specify it). - Liam
DeleteThis is very impressive. Do you think there will be a way to expand this method to also model the relative proportion of different states? So not just A+B, but 40% A, 60% B? I guess such proportions would make the function very computationally challenging, right?
ReplyDeleteMark - this would be really cool, right? Unfortunately, within the current framework its a bit complicated....
DeleteHi, Liam!
ReplyDeleteIt's Patricia, I don't know if you remember me but we met at the Maldonado course (I am the girl who works with climbing plants). I was trying to plot the pie charted phylogeny for a 4-state character and kept getting an error right after trying to plot the little pie charts. Can you maybe help me? Here's the code with the error message:
###
> plotTree(climber.tree,ftype="off",lwd=1,type="fan")
> X<-strsplit(setNames(as.character(Mechs),names(Mechs)),"+",fixed=TRUE)
> pies<-matrix(0,Ntip(climber.tree),4,dimnames=list(climber.tree$tip.label,c("1","2","3","4")))
> for(i in 1:Ntip(climber.tree))
+ pies[climber.tree$tip.label[i],X[[climber.tree$tip.label[i]]]]<-rep(1/length(
+ X[[climber.tree$tip.label[i]]]),length(X[[climber.tree$tip.label[i]]]))
> tiplabels(pie=pies,piecol=c("black","yellow","red","blue"),cex=0.2)
Error in seq.default(x[i], x[i + 1], length = n) :
'to' must be a finite number
> legend(x="topleft",legend=c("Leaning","Root climbing","Main stem twining",
+ "Prehensile/Twining structures"),pt.cex=2,pch=21,
+ pt.bg=c("black","yellow","red","blue"))
###
Everything else but the pie charts is plotted. Any light you can give me will be much appreciated.
Thank you so much!
Best,
Hi Patricia.
DeleteYes, I remember you.
Does your data contain polymorphism (i.e., more than one state at some tips containing a "+" to separate the two or more states)? That is what the strsplit line is for.
Does the pies matrix look right? I.e., does it contain a 1.0 under the corresponding state for every tip - and a 0.5 0.5 (if two states) for every bimorphic taxon?
Other than these simple checks I would need to see the tree & data. Please feel free to email me the files & a minimum script to reproduce the error & I would be happy to look into it.
- Liam
Hi Liam,
DeleteWell, it seems like I'm gonna have to email you the files, the pies matrix has only zeros in it and I have no idea what happened.
I'll send it to you in a moment.
Thank you!
Dear Liam,
ReplyDeleteI was wondering how/if you can alter the design matrix for the fitpolyMK models. Currently I have a dataset where A, B, C, B+C are options, but A+B and A+C not (A+C is not opted in the matrix design, but A+B is, though both are not in the data). Because not all options in the design matrix are in the actual data I get a 'subscript out of bounds' error. Do you know how you can alter the design matrix to correct for these missing options?
Big thanks in advance!
Dear Vicky.
DeleteIt's not necessary to have all levels in the data for them to be included in the model.
Do you want A+B in the model, or just B+C?
In other words, do you hypothesize that to get from A to B evolution must go through A+B. If so, it can be included in your model (even if it is not observed).
In summary: [1] your 'subscript out of bounds' error is probably not due to A+B not being in your data; [2] if you want A+B in your model, that's fine -- if not, you will need to write your own custom model.
To write a custom model please email me & I will send you a worked example.
-- Liam
Dear Liam,
DeleteFirst of all thanks for the quick reply!
I also thought it was unnecessary to have all levels in the data. Turned out it was a silly data framing mistake; I took a subset of the data because there are some missing values for some characters, and this was read wrong by r... Anyway, it works now.
Thank you for leading me to the solution! And a big thanks to your wonderful blogs!!!
All the best,
Vicky