M<-btree$Nnode
N<-length(btree$tip)
anc<-vector()
for(i in 1:M+N){
anc[i-N]<-ace(x,multi2di(root(btree,node=i)), method="pic")$ace[1]
names(anc)[i-N]<-i
}
N<-length(btree$tip)
anc<-vector()
for(i in 1:M+N){
anc[i-N]<-ace(x,multi2di(root(btree,node=i)), method="pic")$ace[1]
names(anc)[i-N]<-i
}
Obviously, although this function is designed as a faster version of ace(...,type="continuous",method="ML"), the function actually runs by using many calls to ace(...,method="pic")!!
The object name btree in this code is used to denote binary tree. This highlights the fact that, obviously, contrasts can only be computed for bifurcating trees. We would still like our function to run, though, if the tree contains multifurcating. The remainder of the function code is dedicated to, first, changing a multifurcating tree to a bifurcating one; and then, after computing ancestral states using the code given above, lining up the nodes on the binary tree to the nodes of the original tree containing multifurcations.
The way a did this is a little ad hoc, but it seems to work. I basically went through all the nodes on both the binary and multifurcating tree and, for each node, pulled out a list of all the descendant tips. Then, I used these lists of descendant tips to match nodes between trees.
The code for this function, fastAnc, is here. Let's try it and compare to both ape::ace and phytools::anc.ML.
> library(phytools)
> # first, simulate bifurcating tree & data
> tree<-rtree(200)
> x<-fastBM(tree)
> # now load the source & estimate states with each function
> source("fastAnc.R")
> system.time(res1<-ace(x,tree,method="ML")$ace)
user system elapsed
19.69 0.05 20.38
> system.time(res2<-anc.ML(tree,x,maxit=10000)$ace)
user system elapsed
236.67 0.34 255.00
> system.time(res3<-fastAnc(tree,x))
user system elapsed
2.60 0.00 2.98
> # plot to compare
> par(mfrow=c(2,1),mai=c(1.02,0.82,0.1,0.1))
> plot(res1,res3,xlab="ace",ylab="fastAnc")
> plot(res2,res3,xlab="anc.ML",ylab="fastAnc")
> # first, simulate bifurcating tree & data
> tree<-rtree(200)
> x<-fastBM(tree)
> # now load the source & estimate states with each function
> source("fastAnc.R")
> system.time(res1<-ace(x,tree,method="ML")$ace)
user system elapsed
19.69 0.05 20.38
> system.time(res2<-anc.ML(tree,x,maxit=10000)$ace)
user system elapsed
236.67 0.34 255.00
> system.time(res3<-fastAnc(tree,x))
user system elapsed
2.60 0.00 2.98
> # plot to compare
> par(mfrow=c(2,1),mai=c(1.02,0.82,0.1,0.1))
> plot(res1,res3,xlab="ace",ylab="fastAnc")
> plot(res2,res3,xlab="anc.ML",ylab="fastAnc")
Obviously, we get the same estimates from each function - but at much greater computational cost (particularly for anc.ML, which is pretty terrible).
That was for a fully bifurcating tree. We can also do a smaller example to make sure we are back-translating our node IDs correctly. Let's try it:
> tree<-rtree(12)
> # collapse two shortest branches into multifurcations
> tree<-di2multi(tree,tol= sort(tree$edge.length[tree$edge[,2]>length(tree$tip)])[3])
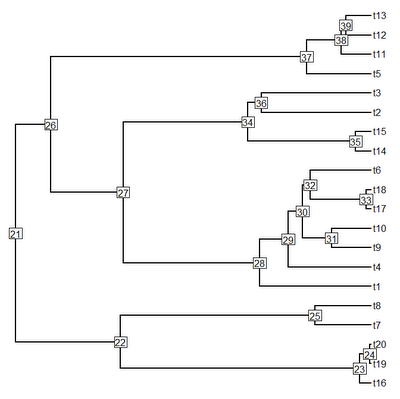
> plot(tree,no.margin=TRUE); nodelabels()
> # collapse two shortest branches into multifurcations
> tree<-di2multi(tree,tol= sort(tree$edge.length[tree$edge[,2]>length(tree$tip)])[3])
> plot(tree,no.margin=TRUE); nodelabels()
> # simulate data
> x<-fastBM(tree)
> # estimate ancestral states using the three methods
> res1<-ace(x,tree,method="ML")$ace
Error in ace(x, tree, method = "ML") :
"phy" is not rooted AND fully dichotomous.
> res2<-anc.ML(tree,x)$ace
> res3<-fastAnc(tree,x)
> par(mai=c(1.02,0.82,0.2,0.2))
> plot(res2,res3,xlab="anc.ML",ylab="fastAnc")
> res2
13 14 15 16 17
0.28663746 0.05138613 -0.25089177 0.50494223 0.13529718
18 19 20 21
0.03920500 0.49088849 1.24192050 1.63727735
> res3
13 14 15 16 17
0.28665585 0.05139666 -0.25089395 0.50494620 0.13528936
18 19 20 21
0.03920408 0.49088277 1.24191236 1.63727663
> x<-fastBM(tree)
> # estimate ancestral states using the three methods
> res1<-ace(x,tree,method="ML")$ace
Error in ace(x, tree, method = "ML") :
"phy" is not rooted AND fully dichotomous.
> res2<-anc.ML(tree,x)$ace
> res3<-fastAnc(tree,x)
> par(mai=c(1.02,0.82,0.2,0.2))
> plot(res2,res3,xlab="anc.ML",ylab="fastAnc")
> res2
13 14 15 16 17
0.28663746 0.05138613 -0.25089177 0.50494223 0.13529718
18 19 20 21
0.03920500 0.49088849 1.24192050 1.63727735
> res3
13 14 15 16 17
0.28665585 0.05139666 -0.25089395 0.50494620 0.13528936
18 19 20 21
0.03920408 0.49088277 1.24191236 1.63727663
First off - ace doesn't work at all if the tree is not bifurcating (not sure why this is). anc.ML works fine, but will be very slow for large trees (as we've discovered). fastAnc gives the same estimates and node names - even though it had to first convert to a bifurcating tree, and then back-translate the node numbers. Great!