Locating the phylogenetic postion of the Yeti: Placing cryptic, recently extinct, or hypothesized taxa in an ultrametric phylogeny using continuous character data

I recently returned from teaching in the AnthroTree 2014 Workshop. This is a course organized by Charlie Nunn that is designed to (in brief) introduce anthropologists to basic & advanced methods in phylogenetic comparative biology.

Well, I won't get into too many details, but a grad student in the workshop was interested in placing a hypothesized taxon into an ultrametric phylogeny when she had only continuous character data for this focal species, along with the same characters measured for all the other species in the phylogeny. This turns out to be not a very hard problem. It has the following parts:

(1) Computing the likelihood of continuous character data on a tree. This is not hard. We can just use the method of Felsenstein (1973), which is actually exactly equivalent to computing the likelihood of a Brownian motion model on our tree using standard comparative method machinery.

(2) Accounting for correlations among characters. This is important when the tree is unknown - but in this case we have a base tree containing all but one of our taxa. This makes accounting for correlations among characters in our likelihood calculation quite straightforward. We can just rotate our data using phylogenetic PCs obtained via PCA on the N - 1 tips in our base tree. We then compute the scores for all the taxa in the tree, and the taxon of unknown phylogenetic affinity. Finally, our log-likelihood just becomes the summed log-likelihoods of each of these now evolutionarily orthogonal characters.

(3) Finding the ML tree. Well, unlike the problem of ML optimization from continuous characters when the tree is unknown, this just involves - at worst - optimizing the position of the new branch along each of the 2(N - 2) edges in our base tree, and then picking the edge and position that maximized the likelihood. In reality, we can probably just compute the likelihood from the midpoint of each edge, and then narrow our search to a much smaller set of edges which we search more thoroughly. We only have to find the divergence point because our tree is ultrametric and our new taxon is (we have assumed) extant.

Graham Slater suggested this method be called (facetiously, of course) locate.yeti, and I have just now posted code for this on the phytools page. Here's a quick demo of just how well it works:

## load required packages
require(phytools)
require(phangorn)
require(mnormt)

## load source
source("locate.yeti.R")

## simulate tree & data
N<-50 ## taxa in base tree
m<-10 ## number of continuous characters
## simulate tree
tt<-tree<-pbtree(n=N+1,tip.label=sample(c(paste("t",1:N,
  sep=""),"Yeti")))
## generate a covariance matrix for simulation
L<-matrix(rnorm(n=m*m),m,m)
L[upper.tri(L,diag=FALSE)]<-0
L<-L-diag(diag(L))+abs(diag(diag(L)))
V<-L%*%t(L)
X<-sim.corrs(tree,vcv=V)
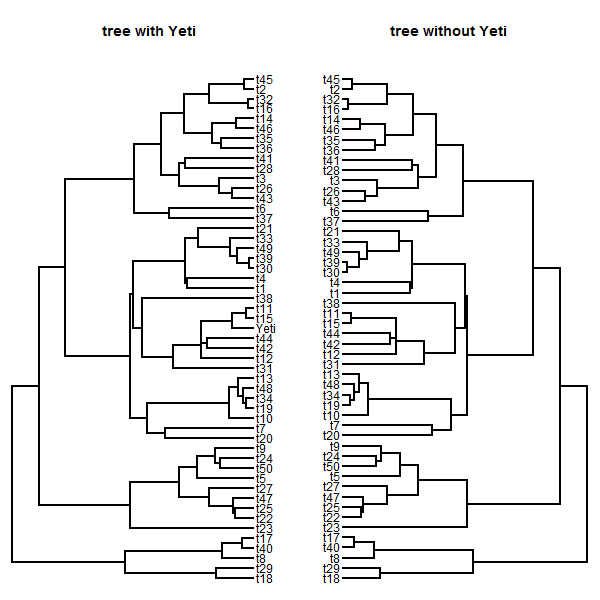
## visualize trees
par(mfrow=c(1,2))
plotTree(tt,mar=c(0.1,0.1,4.1,0.1))
title("tree with Yeti")
tree<-drop.tip(tree,"Yeti")
plotTree(tree,mar=c(0.1,0.1,4.1,0.1),direction="leftwards")
title("tree without Yeti")

## run locate.yeti
mltree<-locate.yeti(tree,X,plot=T)

(This plot shows the likelihood of attaching the tip to any edge.)

## plot results
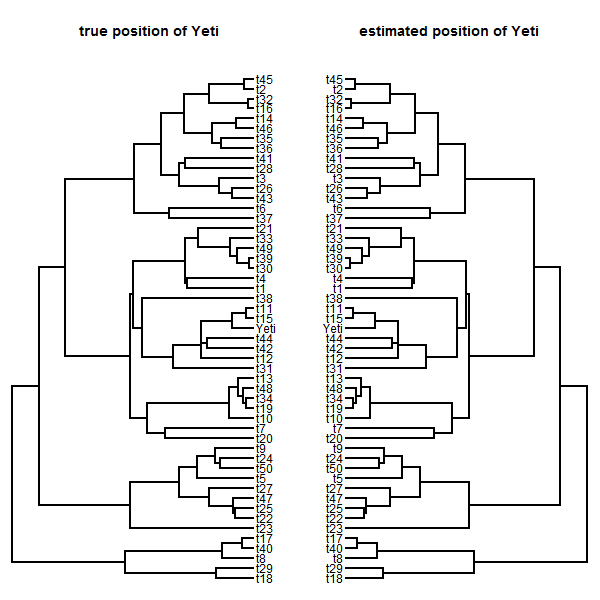
par(mfrow=c(1,2))
plotTree(tt,mar=c(0.1,0.1,4.1,0.1))
title("true position of Yeti")
plotTree(mltree,mar=c(0.1,0.1,4.1,0.1),
  direction="leftwards")
title("estimated position of Yeti")

## compute RF distance
RF.dist(tt,mltree)
## [1] 0

(Of course, it doesn't always do this well!)

In my optimization routine, I take the single edge with the highest likelihood from step one, and then get its parent (if one exists) and daughter (likewise) edges. Then I perform numerical optimization of the position of the cryptic lineage on each of these one, two, three, or more edges. Finally, I pick the edge & location with the highest likelihood. It is, of course, possible that an edge with the cryptic taxon at its midpoint might have an even higher likelihood if that taxon was placed somewhere else along the edge, so this would be the next natural step in expanding this heuristic to have better confidence that we have found the ML position.

Finally, there is no theoretical difficulty in using the same general approach to place a fossil taxon on the tree. In that case we just have one additional parameter to optimize - the terminal edge length. Similarly, we could also using a Bayesian MCMC approach to (say) put prior probabilities on the edges that are more or less likely to have produced our cryptic or fossil lineage.

That's it for now.