Two years of blogging

Just as the title of this post would suggest, phytools blog is two years old** today. (**More or less - as I noted last year, I had a few earlier placeholder posts, but my first serious entry was dated Dec. 24, 2010; and I first advertised this new blog via the now defunct dechronization blog the next day.)

In two years of blogging I have created over 320 posts. Obviously, some entries are very brief - maybe just a few words about a bug fix or report. In others, I was more in depth - for instance, when I wrote about the difficulty of estimating phylogenetic signal on very small trees; or when I discussed how to include fossil phenotypes in the estimation of ancestral states. If printed as a book (and, who knows, perhaps it will one day form the basis for one), the phytools blog would be a dense tome containing over 350 pages. Yikes!

The phytools blog has also grown in popularity over the past year. Raw "pageview" counts can be affected by many things, and are thus difficult to interpret, but phytools blog has received over 90,000 pageviews since it's creation - over 60,000 in the past year. By any measure, that rate is growing - and this also equates to over 160 pageviews/day for 2012. Among the posts accruing the greatest number of pageviews in 2012: my series on xkcd style trees (e.g., 1, 2, 3); my entries on visualizing trait evolution on trees using colors (e.g., 1, 2); and my posts about ancestral character estimation under the threshold model from quantitative genetics (e.g., 1, 2, 3).

The phytools package (also on CRAN) has grown as well. From a small hodgepodge of methods, phytools has grown into a big one - now containing over 80 different functions and a PDF manual that (as of latest CRAN release) contained 87 pages.

Towards the end of 2012, phytools blog got a new look. Since when the original visual theme was created, phytools had no plotting functions (but now it has tons), this seemed appropriate. The blog also got a new URL (after I obtained the domain phytools.org).

I don't doubt for a second that 2013 will be just as productive as 2012 - so thanks for reading, and please keep coming back. Happy holidays!

Specifying pie colors in ancThresh & plotThresh

A phytools user contacted me to express difficulty in controlling pie colors at nodes using the new phytools functions for ancestral character estimation under the threshold model, ancThresh and plotThresh. This is done using the argument piecol, set to a vector with the states for the discrete trait as names, and the desired colors as values (in any format acceptable by R, e.g., here).

Here's a quick demo. I assume that we've already run the MCMC, and mcmc is the object returned by ancThresh. Data are in X:

> cols
   not     mod    high
"green"  "blue"   "red"
> plotThresh(tree,X,mcmc,piecol=cols,tipcol="estimated", label.offset=0.01)

Note that label.offset is on the scale of your phylogeny, so will have to be varied with total tree length. I've been meaning to migrate control of the pie sizes to the user, but have not yet had time to do so. (Plus, I've been sick.)

Plotting densityMap to PDF

A phytools user asks:
In the densityMap graphic you sent me it seemed like you had spread the branches apart some to make the tree more readable. Is that true? If so, could you tell me how?! I have attached a graphic I made and it looks terrible. . . .

Indeed it did look terrible.

In fact, there was really no mystery to how I used the same function to make a "nice" looking figure - I just used the 'grDevices' function pdf to plot directly to a PDF. This means I can set the dimensions of the plot to be anything I like, and squidged up branches and tip labels in an R plotting window will look nice!

Here's a quick example, using contMap (because densityMap is slow for large trees):

> tree<-pbtree(n=150)
> x<-fastBM(tree)
> pdf(file="contMap.pdf",height=14,width=5)
> # now the output of a plotting call will go to my PDF
> contMap(tree,x,outline=FALSE,fsize=c(0.6,1), lims=c(floor(range(x)[1]*10)/10,
ceiling(range(x)[2]*10)/10))
> # you can probably ignoring the "lims" argument
> # I've just used it here to get a nicer legend
> dev.off()
null device
          1

And here's the result (pulled from the PDF - obviously reduced in quality as a result):

New version of threshDIC

I just posted a new version of threshDIC for computing the Deviance Information Criterion from the object returned by ancThresh. The previous version (of threshDIC not ancThresh) just plain doesn't work. I made some mistakes on key calculations that are now fixed.

DIC is in some ways analogous to the Akaike Information Criterion (AIC), but provides the advantage that it can be used on the results of an MCMC chain - and thus doesn't not require that we can analytically or numerically solve for the maximum of the likelihood function.

The deviance is just -2 × the log-likelihood; and DIC requires that we calculate to versions of this - the mean deviance across samples (Dbar), and deviance at the mean parameter values from the posterior sample (Dhat. We penalize our IC by computing the effective number of parameters of the model (pD or pV, depending on the method we want to use).

Here's a quick demo for the dataset and tree I used earlier:

> require(phytools)
> threshDIC(tree,X,mcmc,sequence=c("not","mod","high"))
    Dbar      Dhat        pD       DIC
-21.29781 -68.07082  46.77302  25.47521

Just like with AIC, we should generally prefer the model with the lowest DIC - although DIC differences of less than 5-10 are difficult to interpret.

The new function is here, but I would advise downloading the latest version of phytools (phytools 0.2-15) and installing from source if you want to use this function:

> install.packages("phytools_0.2-15.tar.gz",type="source", repos=NULL)

Function setNames

I can't believe I just discovered the function setNames in the 'stats' package. All it is is a wrapper to combine the two lines of code required to create a vector & assign its names. (It can also be used to add names to other objects, such as a list.) So, for instance, instead of:

> x<-c(1:3)
> names(x)<-c("one","two","three")
> x
 one   two three
   1     2     3

We can do:

> x<-setNames(c(1:3),c("one","two","three"))
> x
 one   two three
   1     2     3

How have I been living without this for so long!

Faster inversion of square symmetric positive-definite matrices

For square, symmetric, positive-definite matrices (like covariance matrices) there is a method for faster matrix inversion that uses inversion of the Cholesky matrix. This is described here and implemented in the R package "Matrix". Here's a quick example, using the phylogenetic covariance matrix (vcv.phylo):

> require(phytools)
> # simulate tree
> tree<-pbtree(n=2000)
> C<-vcv(tree)
> # using solve
> system.time(Cinv1<-solve(C))
  user  system elapsed
 15.15    0.07   15.23
> system.time(Cinv2<-chol2inv(chol(C)))
  user  system elapsed
  6.69    0.02    6.74
> mean(abs(Cinv2-Cinv1))
[1] 3.953766e-16

That's faster.

Hypothesis testing using fitDiversityModel

A user had this question about using the function fitDiversityModel (which implements an ML version of the method in Mahler et al. (2010) to test hypotheses about phenotypic diversification:

I have one short question. In the paper by L. Mahler & al. they also tested the model with a single evolutionary rate. I’m asking me if it is “enough” to write it like that: Constant.time.results <- fitDiversityModel(tree,x,d=NULL)

The answer is "no" - but it is very easy to conduct the desired test. If fitDiversity(...,d=NULL), then the function estimates lineage density at each node as if the radiation is occurring within a single region (and there is no extinction or missing taxa - but that is a matter for another day); and then fits a model in which the rate of evolution varies as a function of lineage density. This will generally not be our null model. For that, we should specify d to be a vector of zeroes. We can then use a likelihood ratio test (for example) to test the null hypothesis that the pace of evolution has declined with increasing lineage density.

Here's a worked example, simulated so that the null is correct:

> require(phytools)
> # simulate tree & data under the null
> tree<-pbtree(n=100)
> x<-fastBM(tree)
> # fit the lineage-density model assuming a single region
> # (i.e., all contemporary ancestors were competitors)
> fitLD<-fitDiversityModel(tree,x)
no values for lineage density provided; computing assuming single biogeographic region
> fitLD
$logL
[1] -126.7954
$sig0
[1] 1.171704
$psi [1] -0.004116475
$vcv
            sig0           psi
sig0  0.121592376 -1.833989e-03
psi  -0.001833989  3.240988e-05

> # now fit the null hypothesis of constant rate
> d<-rep(0,tree$Nnode); names(d)<-1:tree$Nnode+length(tree$tip)
> fitNull<-fitDiversityModel(tree,x,d)
psi not estimable because diversity is constant through time.
> fitNull
$logL
[1] -127.0581
$sig0
[1] 0.9602251
$vcv
            sig0
sig0 0.01844064

> # now test using LR
> LR<-2*(fitLD$logL-fitNull$logL)
> P<-pchisq(LR,df=1,lower.tail=F)
> P
[1] 0.4685722

The null model is just pure Brownian motion; and we would obtain the same parameter estimate and likelihood using, say, fitContinuous in the geiger package:

> fitContinuous(tree,x)
Fitting BM model:
$Trait1
$Trait1$lnl
[1] -127.0581
$Trait1$beta
[1] 0.9602253
$Trait1$aic
[1] 258.1161
$Trait1$aicc
[1] 258.2411
$Trait1$k
[1] 2

That's it.

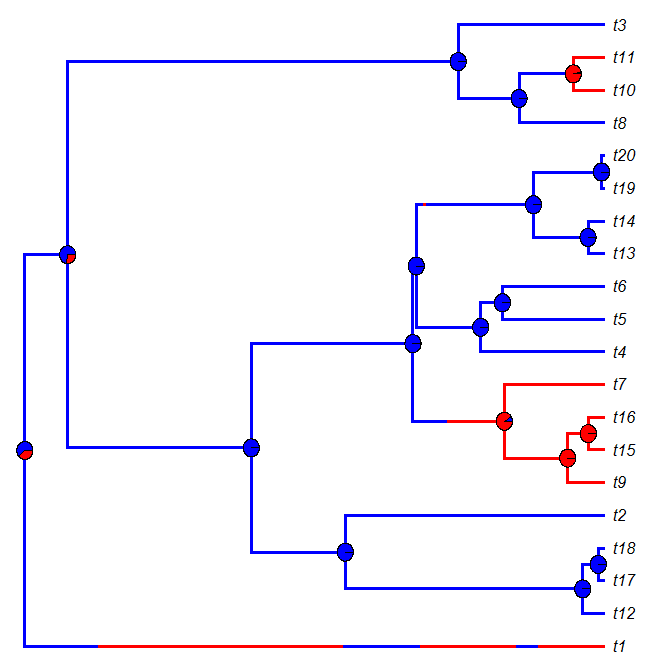
Plotting node piecharts on top of a plotSimmap tree

Today a user asked:

I was wondering: is it possible to use nodelabels(pie=data,cex=0.4) from ape to draw piecharts on top of the plotSimmap (at nodes)? I've tried a bit with the default settings, but it didn't do a good job with placing piecharts at correct nodes. Changing margins didn't help too.

plotSimmap and plot.phylo use totally different coordinate systems; in addition, plot.phylo returns its settings invisibly to the environment - settings that are in turn used by helper functions like nodelabels. Consequently, I expected that this would be impossible, or at least difficult. As it turns out, it is only the latter (i.e., difficult, not impossible).

The solution (a hack) relies on two key ingredients: transforming the SIMMAP trees to the scale that is used internally by plotSimmap; and, secondly, first calling plot.phylo(...,plot=FALSE), which opens a plotting device and tells R a tree has been plotted, even though one has not. The rest, I figured out by tinkering!

Here is the solution - by way of simulated example. Within this example, I also show how to compute the relative frequency of node states in a set of stochastic mapped trees (after all, what else would we want to plot at internal nodes):

# code to simulate a tree & data
# and to perform stochastic mapping
tree<-pbtree(n=20)
Q<-matrix(c(-1,1,1,-1),2,2)
colnames(Q)<-rownames(Q)<-c(0,1)
x<-sim.history(tree,Q,anc="0")$states
mtrees<-make.simmap(tree,x,nsim=100)
# end simulation code

# function to compute the states
foo<-function(x){
  y<-sapply(x$maps,function(x) names(x)[1])
  names(y)<-x$edge[,1]
  y<-y[as.character(length(x$tip)+1:x$Nnode)]
  return(y)
}
XX<-sapply(mtrees,foo)
pies<-t(apply(XX,1,function(x,levels,Nsim) summary(factor(x,levels))/Nsim,levels=c("0","1"),Nsim=100))
# done computing the states

# code to plot the tree
mtrees<-rescaleSimmap(mtrees,1)
cols<-c("blue","red"); names(cols)<-c(0,1)
par(mar=rep(0.1,4))
plot.phylo(mtrees[[1]],plot=FALSE,no.margin=T)
plotSimmap(mtrees[[1]],cols,pts=FALSE,lwd=3,ftype="off", add=TRUE)
text(1,1:length(mtrees[[1]]$tip),mtrees[[1]]$tip.label, pos=4,font=3)
nodelabels(pie=pies,cex=0.6,piecol=cols)
# done plotting

And here is the result of one such simulation & plotting exercise:

For fun, let's compare this to densityMap:

> densityMap(mtrees,lwd=6)
sorry - this might take a while; please be patient

Cool.

"Recent Comments" widget back

For a few weeks the blogger.com "Recent Comments" gadget has been broken so I pulled it from my sidebar. Today I decided to track down some 3rd party code and "Recent Comments" is back online! (See the sidebar.) Comments are always appreciated & welcome (and at least as likely to get a quick response as an email - which, unfortunately, is not as likely as I'd wish).

Ancestral character estimation under the threshold model: an example

I just posted a new version of the phytools function ancThresh for ancestral character estimation using the threshold model from quantitative genetics. Under the threshold model evolution is of an unknown, and unobserved, continuous character, "liability." When liability exceeds a particular value (the threshold or one of multiple thresholds) the observed, discretely valued character trait changes state. (See the following link for much more discussion of the threshold model on this blog.)

The most significant change from prior versions of the function is that the present version can accept either a vector of length N containing a fixed set of trait values for the tips (as before) or a matrix of dimension N × m (for m conditions of the discrete character) in which the i,jth element contains the prior probability of tip i being in state j. This is not equivalent to modeling within-species polymorphism. Rather we allow the possibility that a tip state is unknown, or that it can be called in one condition or another with definable probability.

I have also added the function plotThresh. This function plots the posterior probabilities of ancestral states on the tree. It is called internally (by default) in ancThresh - but also can be called on its own and given the posterior sample from an MCMC run.

Here's a quick example using the phylogeny of Centrarchidae in Near et al. (2005) and the data for feeding mode (including uncertainty) from Collar et al. (2009). Note that for taxa missing from the Collar et al. study I have assigned states for feeding mode based on the behavior of close relatives - I could have equally well decided that feeding mode was unknown for those species.

> tree<-read.tree("Centrarchidae.tre")
> X<-read.csv("Centrarchidae.csv",header=T,row.names=1)
> X
                           not    mod   high
Acantharchus_pomotis     0.0000 1.0000 0.0000
Lepomis_gibbosus         1.0000 0.0000 0.0000
Lepomis_microlophus      1.0000 0.0000 0.0000
Lepomis_punctatus        1.0000 0.0000 0.0000
Lepomis_miniatus         0.5000 0.5000 0.0000
...
Ambloplites_ariommus     0.3333 0.3333 0.3333
...
> mcmc<-ancThresh(tree,X,ngen=1000000,control= list(piecol=cols,tipcol="estimated"),label.offset=0.01)
**** NOTE: no sequence provided, column order in x
MCMC starting....
gen 1000
gen 2000
....
> layout(c(1,2),heights=c(0.9,0.1))
> plotThresh(tree,X,mcmc,piecol=cols,tipcol="estimated", label.offset=0.01)
> plot.new()
> plot.window(xlim=c(0,10),ylim=c(-2,1.25))
> points(0.2,1,pch=19,col="green",cex=2)
> text(0.2,1,"non-piscivorous",pos=4,offset=0.7)
> points(0.2,0,pch=19,col="blue",cex=2)
> text(0.2,0,"moderately piscivorous",pos=4,offset=0.7)
> points(0.2,-1,pch=19,col="red",cex=2)
> text(0.2,-1,"highly piscivorous",pos=4,offset=0.7)

Note that plotThresh(...,tipcol="estimated") uses the sampled liabilities for tips from the MCMC to obtain posterior probabilities for the trait values of uncertain tips. I could also using plotThresh(...,tipcol="input") to get back the input probabilities.

Well, that's pretty cool. Since there are whole bunch of helper functions that are called internally by ancThresh and plotThresh, I would strongly advise installing the latest minor phytools build (phytools 0.2-14) - rather than loading the source code directly - if you are interested in repeating the analyses of this post. Word of caution (!) - ancThresh is still in very early development (and should be treated as such).

Plot outline-only tree

I realized after posting yesterday that the same trick could be used to plot a pure "outline" tree (i.e., white edges outlined in black). Here's how, using the centrarchid tree of Near et al. (2005):

> # set line widths
> lwd.outer=9; lwd.inner=5
> par(col="white") # font color white
> plotTree(tree,lwd=lwd.outer,ftype="i")
> par(col="black") # reset
> # now the tricky part: create a "fake" mapping
> maps<-tree$edge.length
> maps<-as.list(maps)
> for(i in 1:length(maps)) names(maps[[i]])<-"1"
> cols<-"white"; names(cols)<-"1"
> tree$maps<-maps
> plotSimmap(tree,cols,lwd=lwd.inner,pts=F,add=T,ftype="i", offset=0.2*lwd.outer/3+0.2/3)

That's it.

Plotting an outline around a stochastic character mapped tree

In the functions contMap and densityMap I introduced the option of "outlining" the plotted edges with a fine black line (e.g., described here). It is also now possible to do this with typical stochastic mapped trees using plotSimmap, although not as a built-in option. Here's a quick demo (illustrated with simulated data):

> # first simulate tree & data
> Q<-matrix(c(-2,1,1,1,-2,1,1,1,-2),3,3)
> tree<-sim.history(pbtree(n=30,scale=1),Q,anc=1)
> # now plot (modify as desired
> cols<-c("blue","red","green"); names(cols)<-1:3
> lwd.outer=9; lwd.inner=5
> par(col="white") # font color white
> plotTree(tree,lwd=lwd.outer,ftype="i")
> par(col="black") # reset
> plotSimmap(tree,cols,lwd=lwd.inner,pts=F,add=T,ftype="i", offset=0.2*lwd.outer/3+0.2/3)

What we're doing here is not complicated. Basically, the option plotSimmap(...,add=TRUE) (new only in the latest versions of phytools) lets us first create a tree with the edges plotted in plain black; onto which we overlay the slightly finer lines of our plotted stochastic character mapped tree. A neat thing about this technique is that we use white as a mapping color and it doesn't look ridiculous, for instance, using the same tree as before:

> cols<-c("white","red","green"); names(cols)<-1:3
> lwd.outer=9; lwd.inner=5
> par(col="white") # font color white
> plotTree(tree,lwd=lwd.outer,ftype="i")
> par(col="black") # reset
> plotSimmap(tree,cols,lwd=lwd.inner,pts=F,add=T,ftype="i", offset=0.2*lwd.outer/3+0.2/3)

Finally, readers might notice that to specify the outer line widths, I have added a specifically even number to the inner line width (here, 4 - but it could be 2 or 6). This results in the appearance of a line of equal thickness on either side of the plotted tree. If we use an odd number instead, the appearance is a slight shadow. For instance - readers can try the code below:

> cols<-c("blue","red","green"); names(cols)<-1:3
> lwd.outer=9; lwd.inner=6
> par(col="white") # font color white
> plotTree(tree,lwd=lwd.outer,ftype="i")
> par(col="black") # reset
> plotSimmap(tree,cols,lwd=lwd.inner,pts=F,add=T,ftype="i", offset=0.2*lwd.outer/3+0.2/3)

(although there are probably better ways to generate a more pronounced shadow - perhaps the subject of a future post).